Singular Value Decomposition (SVD)

Learning Objectives

• Construct an SVD of a matrix
• Identify pieces of an SVD
• Use an SVD to solve a problem

Overview

Previously, we explored a class of vectors whose directions were left unchanged by a matrix. We found that, for any square matrix, if there existed \(n\) linearly independent eigenvectors, we could diagonalize \(\bf A\) into the form \(\bf{AX = XD}\), where \(\bf X\) is a basis of \(\mathbb{R}^n\), where \(\bf{Ax_i = \lambda_ix_i}\).

A more general factorization is, for any \(m \times n\) matrix, there exists a singular value decomposition in the form \(\bf{AV = U{\Sigma}}\) or \(\bf{A=U{\Sigma}V^T}\). To result in this composition, we require \(\bf U\) as an orthogonal basis of \(\mathbb{R}^m\), \(\bf V\) as an orthogonal basis of \(\mathbb{R}^n\), and \(\bf{\Sigma}\) as an \(m \times n\) diagonal matrix, where \(\bf{Av_i = \sigma_iu_i}\).

• \(\bf U\) is composed of the eigenvectors of \(\bf{AA^T}\) as its columns.
• \(\bf V\) is composed of the eigenvectors of \(\bf{A^TA}\) as its columns.
• \(\bf \Sigma\) is a diagonal matrix composed of square roots of the eigenvalues of \(\bf{A^TA}\) (or \(\bf{AA^T}\)), called singular values.
  • \(\bf{A^TA}\) and \(\bf{AA^T}\) have the same positive eigenvalues, so the square roots of the eigenvalues are also the same.₁
• The diagonal of \(\bf \Sigma\) is ordered by non-increasing singular values and the columns of \(\bf U\), \(\bf V\) are ordered respectively.

In addition, we define a reduced form: \({\bf A} = {\bf U_{R}} {\bf \Sigma_{R}} {\bf V_R}^T\) where \({\bf U_R}\) is an \(m \times k\) matrix, \({\bf V_R}\) is an \(n \times k\) matrix, and \({\bf \Sigma_{R}}\) is an \(k \times k\) diagonal matrix. Here, \(k = \min(m,n)\).

The proof of these claims follows:

Singular Value Decomposition

An \(m \times n\) real matrix \({\bf A}\) has a singular value decomposition of the form

\[{\bf A} = {\bf U} {\bf \Sigma} {\bf V}^T\]

where \({\bf U}\) is an \(m \times m\) orthogonal matrix, \({\bf V}\) is an \(n \times n\) orthogonal matrix, and \({\bf \Sigma}\) is an \(m \times n\) diagonal matrix. Specifically,

• \({\bf U}\) is an \(m \times m\) orthogonal matrix whose columns are eigenvectors of \({\bf A} {\bf A}^T\), called the left singular vectors of \({\bf A}\).

\[\mathbf{A}\mathbf{A}^T = ({\bf U} {\bf \Sigma} {\bf V}^T)({\bf U} {\bf \Sigma} {\bf V}^T)^T\] \[\hspace{2cm} ({\bf U} {\bf \Sigma} {\bf V}^T) ({\bf V}^T)^T {\bf \Sigma}^T {\bf U}^T = {\bf U} {\bf \Sigma} ({\bf V}^T {\bf V}) {\bf \Sigma}^T {\bf U}^T = {\bf U} ({\bf \Sigma} {\bf \Sigma}^T) {\bf U}^T\]

Hence, \(\bf{AA^T=U\Sigma^2U^T}\), which is a diagonalization, where the columns of U are linearly independent.

• \({\bf V}\) is an \(n \times n\) orthogonal matrix whose columns are eigenvectors of \({\bf A}^T {\bf A}\), called the right singular vectors of \({\bf A}\).

\[\mathbf{A}^T\mathbf{A} = ({\bf U} {\bf \Sigma} {\bf V}^T)^T ({\bf U} {\bf \Sigma} {\bf V}^T)\] \[= {\bf V} ({\bf \Sigma}^T {\bf \Sigma}) {\bf V}^T\]

Hence, \(\bf{A^TA=V\Sigma^2V^T}\), which is a diagonalization, where the columns of V are linearly independent.

• \({\bf \Sigma}\) is an \(m \times n\) diagonal matrix, composed of the square root of the eigenvalues of \(A^TA\), in the form:

\[\begin{eqnarray} {\bf \Sigma} = \begin{bmatrix} \sigma_1 & & \\ & \ddots & \\ & & \sigma_s \\ 0 & & 0 \\ \vdots & \ddots & \vdots \\ 0 & & 0 \end{bmatrix} \text{when } m > n, \; \text{and} \; {\bf \Sigma} = \begin{bmatrix} \sigma_1 & & & 0 & \dots & 0 \\ & \ddots & & & \ddots &\\ & & \sigma_s & 0 & \dots & 0 \\ \end{bmatrix} \text{when} \, m < n. \end{eqnarray}\]

where \(k = \min(m,n)\) and \(\sigma_1 \ge \sigma_2 \dots \ge \sigma_s \ge 0\). The diagonal entries are called the singular values of \({\bf A}\).

Obtaining Singular Values

Note that the matrices \(\bf{A^TA}\) and \(\bf{AA^T}\) always have the same non-zero eigenvalues. In addition, they are both positive semi-definite (defined: \(\mathbf{x^{T}Bx} \geq 0 \quad \forall \mathbf{x} \neq 0\)). As the eigenvalues of positive semi-definite matrices are always non-negative, singular values are always non-negative.

If \(\mathbf{A}^T\mathbf{x} \ne 0\), then \(\mathbf{A}^T\mathbf{A}\) and \(\mathbf{A}\mathbf{A}^T\) both have the same eigenvalues:

\[\mathbf{A}\mathbf{A}^T\mathbf{x} = \lambda \mathbf{x}\] \[\mathbf{A}^T\mathbf{A}\mathbf{A}^T\mathbf{x} = \mathbf{A}^T \lambda \mathbf{x}\] \[\mathbf{A}^T\mathbf{A}(\mathbf{A}^T\mathbf{x}) = \lambda (\mathbf{A}^T\mathbf{x})\]

Time Complexity

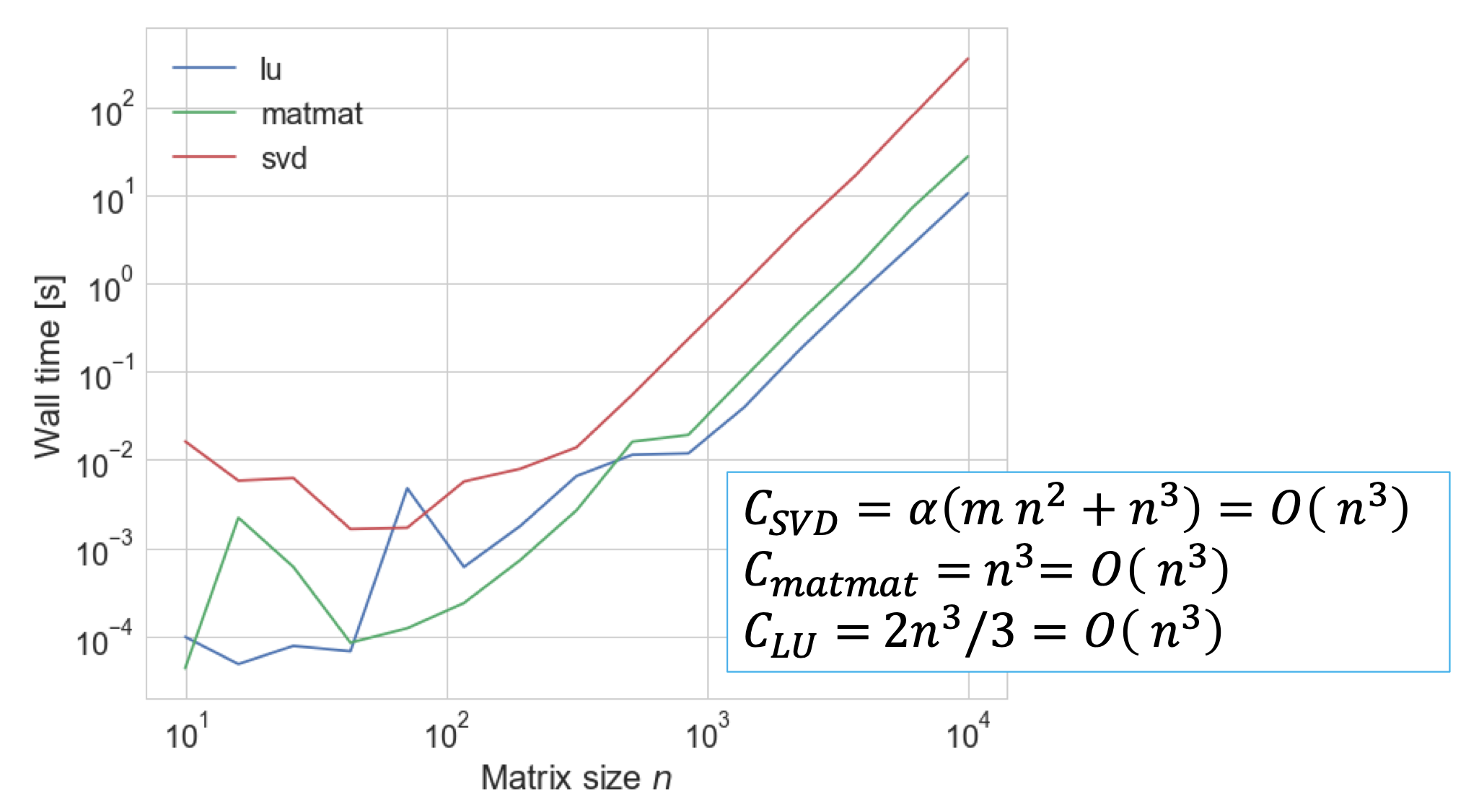
The time-complexity for computing the SVD factorization of an arbitrary \(m \times n\) matrix is \(\alpha (m^2n + n^3)\), where the constant \(\alpha\) ranges from 4 to 10 (or more) depending on the algorithm.

In general, we can define the cost as: \(\mathcal{O}(m^2n + n^3)\)

Reduced SVD

The SVD factorization of a non-square matrix \({\bf A}\) of size \(m \times n\) can be represented in a reduced format:

• For \(m \ge n\): \({\bf U}\) is \(m \times n\), \({\bf \Sigma}\) is \(n \times n\), and \({\bf V}\) is \(n \times n\)
• For \(m \le n\): \({\bf U}\) is \(m \times m\), \({\bf \Sigma}\) is \(m \times m\), and \({\bf V}\) is \(n \times m\) (note if \({\bf V}\) is \(n \times m\), then \({\bf V}^T\) is \(m \times n\))

The following figure depicts the reduced SVD factorization (in red) against the full SVD factorizations (in gray).

In general, we will represent the reduced SVD as:

\[{\bf A} = {\bf U}_R {\bf \Sigma}_R {\bf V}_R^T\]

where \({\bf U}_R\) is a \(m \times k\) matrix, \({\bf V}_R\) is a \(n \times k\) matrix, \({\bf \Sigma}_R\) is a \(k \times k\) matrix, and \(k = \min(m,n)\).

Example: Computing the SVD

We begin with the following non-square matrix, \({\bf A}\)

and we will compute the reduced form of the SVD (where here \(s = 3\)):

(1) Compute \({\bf A}^T {\bf A}\):

\[{\bf A}^T {\bf A} = \left[ \begin{array}{ccc} 174 & 158 & 106 \\ 158 & 197 & 134 \\ 106 & 134 & 127 \\ \end{array} \right]\]

(2) Compute the eigenvectors and eigenvalues of \({\bf A}^T {\bf A}\):

\[\lambda_1 = 437.479, \quad \lambda_2 = 42.6444, \quad \lambda_3 = 17.8766, \\ \boldsymbol{v}_1 = \begin{bmatrix} 0.585051 \\ 0.652648 \\ 0.481418\end{bmatrix}, \quad \boldsymbol{v}_2 = \begin{bmatrix} -0.710399 \\ 0.126068 \\ 0.692415 \end{bmatrix}, \quad \boldsymbol{v}_3 = \begin{bmatrix} 0.391212 \\ -0.747098 \\ 0.537398 \end{bmatrix}\]

(3) Construct \({\bf V}_R\) from the eigenvectors of \({\bf A}^T {\bf A}\):

(4) Construct \({\bf \Sigma}_R\) from the square roots of the eigenvalues of \({\bf A}^T {\bf A}\):

(5) Find \({\bf U}\) by solving \({\bf U}{\bf\Sigma} = {\bf A}{\bf V}\). For our reduced case, we can find \({\bf U}_R = {\bf A}{\bf V}_R {\bf \Sigma}_R^{-1}\). You could also find \({\bf U}\) by computing the eigenvectors of \({\bf AA}^T\).

\[{\bf U} = \overbrace{\left[ \begin{array}{ccc} 3 & 2 & 3 \\ 8 & 8 & 2 \\ 8 & 7 & 4 \\ 1 & 8 & 7 \\ 6 & 4 & 7 \\ \end{array} \right]}^{A} \overbrace{\left[ \begin{array}{ccc} 0.585051 & -0.710399 & 0.391212 \\ 0.652648 & 0.126068 & -0.747098 \\ 0.481418 & 0.692415 & 0.537398 \\ \end{array} \right]}^{V} \overbrace{\left[ \begin{array}{ccc} 0.047810 & 0.0 & 0.0 \\ 0.0 & 0.153133 & 0.0 \\ 0.0 & 0.0 & 0.236515 \\ \end{array} \right]}^{\Sigma^{-1}}\] \[{\bf U} = \left[ \begin{array}{ccc} 0.215371 & 0.030348 & 0.305490 \\ 0.519432 & -0.503779 & -0.419173 \\ 0.534262 & -0.311021 & 0.011730 \\ 0.438715 & 0.787878 & -0.431352\\ 0.453759 & 0.166729 & 0.738082\\ \end{array} \right]\]

We obtain the following singular value decomposition for \({\bf A}\):

Recall that we computed the reduced SVD factorization (i.e. \({\bf \Sigma}\) is square, \({\bf U}\) is non-square) here.

Rank, null space and range of a matrix

Suppose \({\bf A}\) is a \(m \times n\) matrix where \(m > n\) (without loss of generality):

\[{\bf A}= {\bf U\Sigma V}^{T} = \begin{bmatrix}\vert & & \vert & & \vert \\ \vert & & \vert & & \vert \\ {\bf u}_1 & \cdots & {\bf u}_n & \cdots & {\bf u}_m\\ \vert & & \vert & & \vert \\\vert & & \vert & & \vert \end{bmatrix} \begin{bmatrix} \sigma_1 & & \\ & \ddots & \\ & & \sigma_n \\ & \vdots & \\ -& 0& -\end{bmatrix} \begin{bmatrix} - & {\bf v}_1^T & - \\ & \vdots & \\ - & {\bf v}_n^T & - \end{bmatrix}\]

We can re-write the above as:

\[{\bf A} = \begin{bmatrix}\vert & & \vert \\ \vert & & \vert \\ {\bf u}_1 & \cdots & {\bf u}_n \\ \vert & & \vert \\ \vert & & \vert \end{bmatrix} \begin{bmatrix} - & \sigma_1 {\bf v}_1^T & - \\ & \vdots & \\ - & \sigma_n{\bf v}_n^T & - \end{bmatrix}\]

Furthermore, the product of two matrices can be written as a sum of outer products:

\[{\bf A} = \sigma_1 {\bf u}_1 {\bf v}_1^T + \sigma_2 {\bf u}_2 {\bf v}_2^T + ... + \sigma_n {\bf u}_n {\bf v}_n^T\]

For a general rectangular matrix, we have:

\[{\bf A} = \sum_{i=1}^{s} \sigma_i {\bf u}_i {\bf v}_i^T\]

where \(s = \min(m,n)\).

If \({\bf A}\) has \(s\) non-zero singular values, the matrix is full rank, i.e. \(\text{rank}({\bf A}) = s\).

If \({\bf A}\) has \(r\) non-zero singular values, and \(r < s\), the matrix is rank deficient, i.e. \(\text{rank}({\bf A}) = r\).

In other words, the rank of \({\bf A}\) equals the number of non-zero singular values which is the same as the number of non-zero diagonal elements in \({\bf \Sigma}\).

Rounding errors may lead to small but non-zero singular values in a rank deficient matrix. Singular values that are smaller than a given tolerance are assumed to be numerically equivalent to zero, defining what is sometimes called the effective rank.

The right-singular vectors (columns of \({\bf V}\)) corresponding to vanishing singular values of \({\bf A}\) span the null space of \({\bf A}\), i.e. null(\({\bf A}\)) = span{\({\bf v}_{r+1}\), \({\bf v}_{r+2}\), …, \({\bf v}_{n}\)}.

The left-singular vectors (columns of \({\bf U}\)) corresponding to the non-zero singular values of \({\bf A}\) span the range of \({\bf A}\), i.e. range(\({\bf A}\)) = span{\({\bf u}_{1}\), \({\bf u}_{2}\), …, \({\bf u}_{r}\)}.

Example:

\[{\bf A} = \left[ \begin{array}{cccc} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 & 0 \\ \frac{1}{\sqrt{2}}2 &\frac{1}{\sqrt{2}} & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array} \right] \left[ \begin{array}{ccc} 14 & 0 & 0 \\ 0 & 14 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right] \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right]\]

The rank of \({\bf A}\) is 2.

The vectors \(\left[ \begin{array}{c} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ 0 \\ 0 \end{array} \right]\) and \(\left[ \begin{array}{c} -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ 0 \\ 0 \end{array} \right]\) provide an orthonormal basis for the range of \({\bf A}\).

The vector \(\left[ \begin{array}{c} 0 \\ 0\\ 1 \end{array} \right]\) provides an orthonormal basis for the null space of \({\bf A}\).

(Moore-Penrose) Pseudoinverse

If the matrix \({\bf \Sigma}\) is rank deficient, we cannot get its inverse. We define instead the pseudoinverse:

\[({\bf \Sigma}^+)_{ii} = \begin{cases} \frac{1}{\sigma_i} & \sigma_i \neq 0\\ 0 & \sigma_i = 0 \end{cases}\]

For a general non-square matrix \({\bf A}\) with known SVD (\({\bf A} = {\bf U\Sigma V}^T\)), the pseudoinverse is defined as:

\[{\bf A}^{+} = {\bf V\Sigma}^{+}{\bf U}^T\]

For example, if we consider a \(m \times n\) full rank matrix where \(m > n\):

\[{\bf A}^{+}= \begin{bmatrix} \vert & ... & \vert \\ {\bf v}_1 & ... & {\bf v}_n\\ \vert & ... & \vert \end{bmatrix} \begin{bmatrix} 1/\sigma_1 & & & 0 & \dots & 0 \\ & \ddots & & & \ddots &\\ & & 1/\sigma_n & 0 & \dots & 0 \\ \end{bmatrix} \begin{bmatrix}\vert & & \vert & & \vert \\ \vert & & \vert & & \vert \\ {\bf u}_1 & \cdots & {\bf u}_n & \cdots & {\bf u}_m\\ \vert & & \vert & & \vert \\\vert & & \vert & & \vert \end{bmatrix}^T\]

Euclidean norm of matrices

The induced 2-norm of a matrix \({\bf A}\) can be obtained using the SVD of the matrix :

\[\begin{align} \| {\bf A} \|_2 &= \max_{\|\mathbf{x}\|=1} \|\mathbf{A x}\| = \max_{\|\mathbf{x}\|=1} \|\mathbf{U \Sigma V}^T {\bf x}\| \\ & =\max_{\|\mathbf{x}\|=1} \|\mathbf{ \Sigma V}^T {\bf x}\| = \max_{\|\mathbf{V}^T{\bf x}\|=1} \|\mathbf{ \Sigma V}^T {\bf x}\| =\max_{\|y\|=1} \|\mathbf{ \Sigma} y\| \end{align}\]

And hence,

\[\| {\bf A} \|_2= \sigma_1\]

In the above equations, all the notations for the norm \(\| . \|\) refer to the \(p=2\) Euclidean norm, and we used the fact that \({\bf U}\) and \({\bf V}\) are orthogonal matrices and hence \(\|{\bf U}\|_2 = \|{\bf V}\|_2 = 1\).

Example:

We begin with the following non-square matrix \({\bf A}\):

\[{\bf A} = \left[ \begin{array}{ccc} 3 & 2 & 3 \\ 8 & 8 & 2 \\ 8 & 7 & 4 \\ 1 & 8 & 7 \\ 6 & 4 & 7 \\ \end{array} \right].\]

The matrix of singular values, \({\bf \Sigma}\), computed from the SVD factorization is:

Consequently the 2-norm of \({\bf A}\) is

Euclidean norm of the inverse of matrices

Following the same derivation as above, we can show that for a full rank \(n \times n\) matrix we have:

\[\| {\bf A}^{-1} \|_2= \frac{1}{\sigma_n}\]

where \({\sigma_n}\) is the smallest singular value.

For non-square matrices, we can use the definition of the pseudoinverse (regardless of the rank):

\[\| {\bf A}^{+} \|_2= \frac{1}{\sigma_r}\]

where \({\sigma_r}\) is the smallest non-zero singular value. Note that for a full rank square matrix, we have \(\| {\bf A}^{+} \|_2 = \| {\bf A}^{-1} \|_2\). An exception of the definition above is the zero matrix. In this case, \(\| {\bf A}^{+} \|_2 = 0\)

2-Norm Condition Number

The 2-norm condition number of a matrix \({\bf A}\) is given by the ratio of its largest singular value to its smallest singular value:

\[\text{cond}_2(A) = \|{\bf A}\|_2 \|{\bf A}^{-1}\|_2 = \sigma_{\max}/\sigma_{\min}.\]

If the matrix \({\bf A}\) is rank deficient, i.e. \(\text{rank}({\bf A}) < \min(m,n)\), then \(\text{cond}_2({\bf A}) = \infty\).

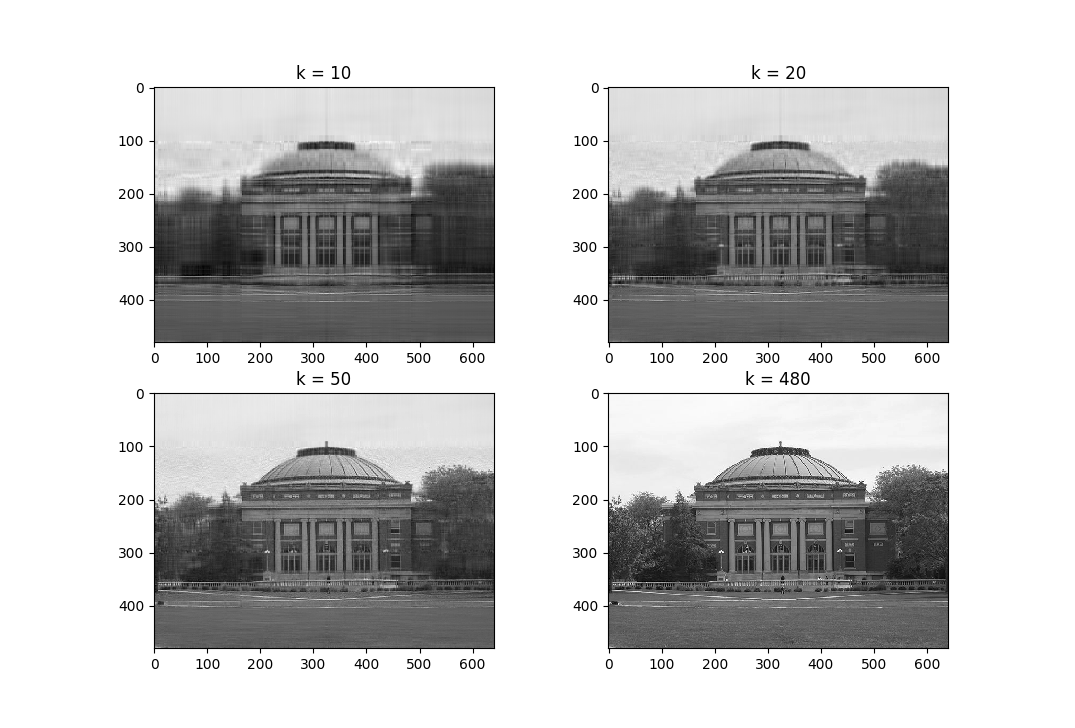
Low-rank Approximation

The best rank-\(k\) approximation for a \(m \times n\) matrix \({\bf A}\), where \(k < s = \min(m,n)\), for some matrix norm \(\|.\|\), is one that minimizes the following problem:

\[\begin{aligned} &\min_{ {\bf A}_k } \ \|{\bf A} - {\bf A}_k\| \\ &\textrm{such that} \quad \mathrm{rank}({\bf A}_k) \le k. \end{aligned}\]

Under the induced \(2\)-norm, the best rank-\(k\) approximation is given by the sum of the first \(k\) outer products of the left and right singular vectors scaled by the corresponding singular value (where, \(\sigma_1 \ge \dots \ge \sigma_s\)):

\[{\bf A}_k = \sigma_1 \bf{u}_1 \bf{v}_1^T + \dots \sigma_k \bf{u}_k \bf{v}_k^T\]

Observe that the norm of the difference between the best approximation and the matrix under the induced \(2\)-norm condition is the magnitude of the \((k+1)^\text{th}\) singular value of the matrix:

\[\|{\bf A} - {\bf A}_k\|_2 = \left|\left|\sum_{i=k+1}^n \sigma_i \bf{u}_i \bf{v}_i^T\right|\right|_2 = \sigma_{k+1}\]

Note that the best rank-\({k}\) approximation to \({\bf A}\) can be stored efficiently by only storing the \({k}\) singular values \({\sigma_1,\dots,\sigma_k}\), the \({k}\) left singular vectors \({\bf u_1,\dots,\bf u_k}\), and the \({k}\) right singular vectors \({\bf v_1,\dots, \bf v_k}\).

The figure below show best rank-\(k\) approximations of an image (you can find the code snippet that generates these images in the IPython notebook):

Using SVD to solve a square system of linear equations

If \(\bf A\) is an \(n \times n\) square matrix and we want to solve \(\bf{Ax=b}\), we can use the svd for A such that

\[\bf{U{\Sigma}V^Tx=b}\] \[\bf{ {\Sigma} V^Tx=U^Tb}\]

Solve: \(\bf{\Sigma y=U^Tb}\) (diagonal matrix, easy to solve)

Evaluate: \(\bf{x=Vy}\)

• Cost of solve: \(O(n^2)\)
• Cost of decomposition \(O(n^3)\). Recall that SVD and LU have the same asymptotic behavior, however the number of operations - the constant factor before the \(n^3\) - for the SVD is larger.

Footnotes

1. See this Math Stack Exchange post for a brief explanation.

Review Questions

• For a matrix \(\bf A\) with SVD decomposition \(\bf{A=U{\Sigma}V^T}\), what are the columns of \(\bf U\) and how can we find them? What are the columns of \(\bf V\) and how can we find them? What are the entries of \(\bf{\Sigma}\) and how can we find them?
• What special properties are true of \(\bf U\), \(\bf V\) and \(\bf{\Sigma}\)?
• What are the shapes of \(\bf U\), \(\bf V\) and \(\bf{\Sigma}\) in the full SVD of an matrix?
• What are the shapes of \(\bf U\), \(\bf V\) and \(\bf{\Sigma}\) and in the reduced SVD of an matrix?
• What is the cost of computing the SVD?
• Given an already computed SVD of a matrix \(\bf A\), what is the cost of using the SVD to solve a linear system \(\bf{Ax=B}\)? How would you use the SVD to solve this system?
• How do you use the SVD to compute a low-rank approximation of a matrix? For a small matrix, you should be able to compute a given low rank approximation (i.e. rank-one, rank-two).
• Given the SVD of a matrix \(\bf A\), what is the SVD of \(\mathbf{A}^+\) (the psuedoinverse of \(\bf A\))?
• Given the SVD of a matrix \(\bf A\), what is the 2-norm of the matrix? What is the 2-norm condition number of the matrix?

Changelog

• November 20th, 2024: Dev Singh (dsingh14) — add more details on singular values
• April 5th, 2024: Pascal Adhikary (pascala2) — add/rewrite overview, proof, solve linear systems
• April 10th, 2022: Yuxuan Chen (yuxuan19) — added svd proof, changed svd cost, included svd summary

• View Remaining Entries

  • April 26th, 2020: Mariana Silva (mfsilva) — adding more details to sections
  • November 14th, 2018: Erin Carrier (ecarrie2) — spelling fix
  • October 18th, 2018: Erin Carrier (ecarrie2) — correct svd cost
  • January 14th, 2018: Erin Carrier (ecarrie2) — removes demo links
  • December 4th, 2017: Arun Lakshmanan (lakshma2) — fix best rank approx, svd image
  • November 15th, 2017: Erin Carrier (ecarrie2) — adds review questions, adds cond num sec, removes normal equations, minor corrections and clarifications
  • November 13th, 2017: Arun Lakshmanan (lakshma2) — first complete draft
  • October 17th, 2017: Luke Olson (lukeo) — outline