Rounding
Learning Objectives
- Understand the rounding options of a non-representable number using the IEEE-754 floating pont standard.
- Measure the error in rounding numbers using the IEEE-754 floating point standard
- Understand catastrophic cancellation in floating point arithmetic
- Predict the outcome of loss of significance in floating point arithmetic
- Make an optimal selection among a group of mathematically equivalent formulae to minimize floating point error
Rounding Options in IEEE-754
Not all real numbers can be stored exactly as floating point numbers. Consider a real number in the normalized floating point form:
\[x = \pm 1.b_1 b_2 b_3 ... b_n ... \times 2^m\]where \(n\) is the number of bits in the significand and \(m\) is the exponent for a given floating point system. If \(x\) does not have an exact representation as a floating point number, it will be instead represented as either \(x_{-}\) or \(x_{+}\), the nearest two floating point numbers.
Without loss of generality, let us assume \(x\) is a positive number. In this case, we have:
\[x_{-} = 1.b_1 b_2 b_3 ... b_n \times 2^m\]and
\[x_{+} = 1.b_1 b_2 b_3 ... b_n \times 2^m + 0.\underbrace{000000...0001}_{n\text{ bits}} \times 2^m\]
Notice that \(x_{-}\) is retrieved by "chopping" all the bits after the \(n^{th}\) bit, and \(x_{+} = x_{-} + {\epsilon}_{m} \times 2^m\), where \({\epsilon}_{m}\) is the machine epsilon.
The process of replacing a real number \(x\) by a nearby machine number (either \(x_{-}\) or \(x_{+}\)) is called rounding, and the error involved is called roundoff error.
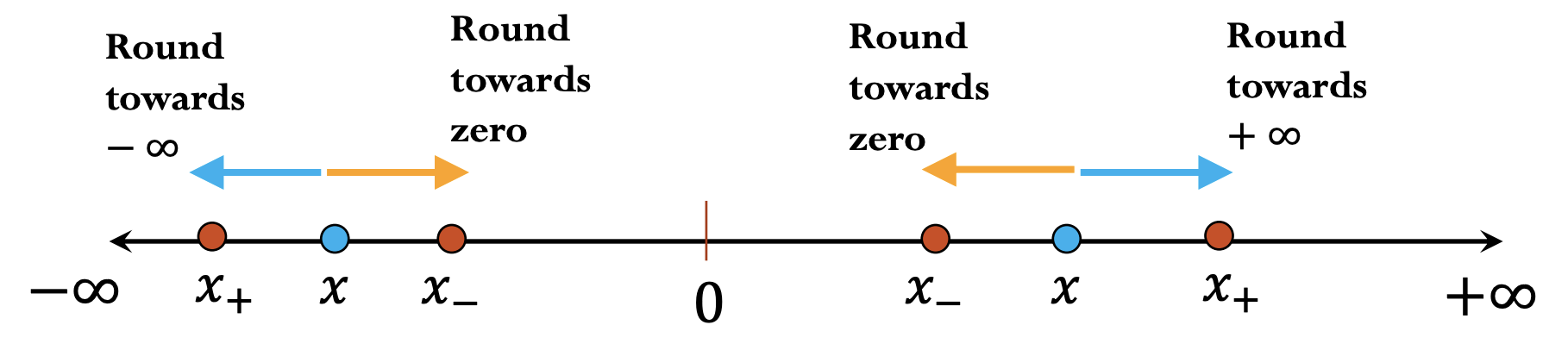
IEEE-754 doesn't specify exactly how to round floating point numbers, but there are several different options:
- round towards zero
- round towards infinity
- round up
- round down
- round to the next nearest floating point number (either round up or down, whatever is closer)
- round by chopping
We will denote the floating point number as \(fl(x)\). The rounding rules above can be summarized below:

round by chopping: \(fl(x) = x_{-}\)
Round-off Errors
For each distinct exponent number \(m \in [L, U]\), the gap between two machine numbers is (notice that \(\epsilon_m\) is the machine epsilon, and is irrelevant with \(m\)):
\[\vert x_{+} - x_{-} \vert = 0.\underbrace{000000...0001}_{n\text{ bits}} \times 2^m = \epsilon_m \times 2^m\]Notice that the interval between successive floating point numbers is not uniform: the interval is smaller as the magnitude of the numbers themselves is smaller, and it is bigger as the numbers get bigger. For example, considering simple precision:
\[x_{+} \hspace{3mm}\text{and}\hspace{3mm} x_{-} \hspace{3mm}\text{of the form}\hspace{3mm} q \times 2^{-10}: \vert x_{+} - x_{-} \vert = 2^{-33} \approx 10^{-10}\] \[x_{+} \hspace{3mm}\text{and}\hspace{3mm} x_{-} \hspace{3mm}\text{of the form}\hspace{3mm} q \times 2^{4}: \vert x_{+} - x_{-} \vert = 2^{-19} \approx 2 \times 10^{-6}\] \[x_{+} \hspace{3mm}\text{and}\hspace{3mm} x_{-} \hspace{3mm}\text{of the form}\hspace{3mm} q \times 2^{20}: \vert x_{+} - x_{-} \vert = 2^{-3} \approx 0.125\] \[x_{+} \hspace{3mm}\text{and}\hspace{3mm} x_{-} \hspace{3mm}\text{of the form}\hspace{3mm} q \times 2^{60}: \vert x_{+} - x_{-} \vert = 2^{37} \approx 10^{11}\]Hence it's better to use machine epsilon to bound the error in representing a real number as a machine number.
Absolute error:
\[\vert fl(x) - x \vert \le \vert x_{+} - x_{-} \vert = \epsilon_m \times 2^m\] \[\vert fl(x) - x \vert \le \epsilon_m \times 2^m\]Relative error:
\[\frac{ \vert fl(x) - x \vert }{ \vert x \vert } \le \frac{ \epsilon_m \times 2^m } { \vert \pm 1.b_1 b_2 b_3 ... b_n ... \times 2^m \vert }\] \[\frac{ \vert fl(x) - x \vert }{ \vert x \vert } \le \epsilon_m\]Using this inequality, observe that for the IEEE single-precision floating point system: \(\frac{ \vert fl(x) - x \vert }{ \vert x \vert } \le 2^{-23} \approx 1.2 \times 10^{-7}\). Since the system consistently introduces relative errors of about \(10^{-7}\), a single precision floating point system typically gives you about 7 (decimal) accurate digits.
Similarly, observe that for the IEEE double-precision floating point system: \(\frac{ \vert fl(x) - x \vert }{ \vert x \vert } \le 2^{-52} \approx 2.2 \times 10^{-16}\). Since the system consistently introduces relative errors of about \(10^{-16}\), a double precision floating point system typically gives you about 16 (decimal) accurate digits.
Example: Determine the rounding error of a non-representable number
If we round to the nearest, what is the double-precision machine representation for 0.1? How much rounding error does it introduce?
Answer
Use the same algorithm that converts a decimal fraction to binary (as introduced in the previous section), we build the following table:| Previous Fractional Part \( \times 2 \) | Integer Part | Current Fractional Part |
|---|---|---|
| 0.2 | 0 | 0.2 |
| 0.4 | 0 | 0.4 |
| 0.8 | 0 | 0.8 |
| 1.6 | 1 | 0.6 |
| 1.2 | 1 | 0.2 |
| 0.4 | 0 | 0.4 |
| 0.8 | 0 | 0.8 |
| 1.6 | 1 | 0.6 |
| 1.2 | 1 | 0.2 |
| ... | ... | ... |
Then, we have \( 0.1 = (0.000110011\hspace{1mm}\overline{0011})_2 = (1.10011\hspace{1mm}\overline{0011})_2 \times 2^{-4}\) .
Rounded by nearest, the double-precision machine representation for 0.1 is the tuple \( (s, c, f) \), where \(s\) is the sign bit, \(c\) is the exponent field, and \(f\) is the significand:
\( s = 0 \)
\( m = -4 \Rightarrow c = m + 1023 = 1019 = 01111111011\)
\( f = 10011...0011...0011010 \)
In other words, the double-precision machine representation for 0.1 is:
\( \bf{0\hspace{2mm}01111111011\hspace{2mm}\underbrace{10011...0011...0011010}_{52\text{ bits}}} \)
The rounding error is then:
\( fl(0.1) - 0.1 = (0.00011001100110011...11010)_2 - (0.00011001100110011...1100110011\overline{0011})_2\) \(= (0.\underbrace{0...0}_{54\text{ 0's}}000110011\overline{0011})_2 = 2^{-54} \times 0.1 = 2^{-2} \times 0.1 \times 2^{-52} = \bf{0.025\epsilon_m}\)
Example: Floating Point Equality
Assume you are working with IEEE single-precision numbers. Find the smallest representable number \(a\) that satisfies \(2^8 + a \neq 2^8\).
Answer
In this class, to approximate the smallest number \(x\) such that \(2^n + x \neq 2^n\), we use the formula \(x = \epsilon_m \cdot 2^n\).Therefore, given that \(\epsilon_m\) for IEEE single-precision is \(2^{-23}\), the answer is \(\bf{a = 2^{-23} \cdot 2^8 = 2^{-15}}\).
Notice that we use the default rounding mode - rounding to the nearest representable value. If the result is midway between two representable values, the even representable is chosen. "Even" means the lowest-order bit is zero.
The smallest representable number larger than \(2^8\) is \((2+\epsilon_m)\times 2^8\).
Let \(x_{-} = 2^8\) and \(x_{+} = (2+\epsilon_m)\times 2^8\).
In order to have \(2^8 + a\) rounded to \(x_{+}\), we must have \(a \gt \frac{\vert x_{+} - x_{-} \vert}{2} = \frac{\epsilon_m\times 2^8}{2} = \frac{2^{-23}\times 2^8}{2} = 2^{-16}\).
The smallest machine representable number greater than \(2^{-16}\) is \((1 + \epsilon_m) \times 2^{-16}\).
Hence \(\bf{a = \bf{(1 + 2^{-23}) \times 2^{-16}}}\).
Example: Uneven Distribution of Floating Point Numbers in any FPS
Consider the small floating point number system \(x = \pm 1.b_1 b_2 \times 2^m \) for \(m \in [-4, 4]\) and \(b_i \in \{0, 1\}\):
Details
\( (1.00)_2 \times 2^{-4} = 0.0625 \)\( (1.01)_2 \times 2^{-4} = 0.078125 \)
\( (1.10)_2 \times 2^{-4} = 0.09375 \)
\( (1.11)_2 \times 2^{-4} = 0.109375 \)
\( (1.00)_2 \times 2^{-3} = 0.125 \)
\( (1.01)_2 \times 2^{-3} = 0.15625 \)
\( (1.10)_2 \times 2^{-3} = 0.1875 \)
\( (1.11)_2 \times 2^{-3} = 0.21875 \)
\( (1.00)_2 \times 2^{-2} = 0.25 \)
\( (1.01)_2 \times 2^{-2} = 0.3125 \)
\( (1.10)_2 \times 2^{-2} = 0.375 \)
\( (1.11)_2 \times 2^{-2} = 0.4375 \)
\( (1.00)_2 \times 2^{-1} = 0.5 \)
\( (1.01)_2 \times 2^{-1} = 0.625 \)
\( (1.10)_2 \times 2^{-1} = 0.75 \)
\( (1.11)_2 \times 2^{-1} = 0.875 \)
\( (1.00)_2 \times 2^{0} = 1.0 \)
\( (1.01)_2 \times 2^{0} = 1.25 \)
\( (1.10)_2 \times 2^{0} = 1.5 \)
\( (1.11)_2 \times 2^{0} = 1.75 \)
\( (1.00)_2 \times 2^{1} = 2.0 \)
\( (1.01)_2 \times 2^{1} = 2.5 \)
\( (1.10)_2 \times 2^{1} = 3.0 \)
\( (1.11)_2 \times 2^{1} = 3.5 \)
\( (1.00)_2 \times 2^{2} = 4.0 \)
\( (1.01)_2 \times 2^{2} = 5.0 \)
\( (1.10)_2 \times 2^{2} = 6.0 \)
\( (1.11)_2 \times 2^{2} = 7.0 \)
\( (1.00)_2 \times 2^{3} = 8.0 \)
\( (1.01)_2 \times 2^{3} = 10.0 \)
\( (1.10)_2 \times 2^{3} = 12.0 \)
\( (1.11)_2 \times 2^{3} = 14.0 \)
\( (1.00)_2 \times 2^{4} = 16.0 \)
\( (1.01)_2 \times 2^{4} = 20.0 \)
\( (1.10)_2 \times 2^{4} = 24.0 \)
\( (1.11)_2 \times 2^{4} = 28.0 \)
Mathematical Properties of Floating Point Operations
- Not necessarily associative: \((x + y) + z \neq x + (y + z)\).
This is because \(fl(fl(x + y) + z) \neq fl(x + fl(y + z))\).
- Not necessarily distributive: \(z \cdot (x + y) \neq z \cdot x + z \cdot y\).
This is because \(fl(z \cdot fl(x + y)) \neq fl(fl(z \cdot x) + fl(z \cdot y))\).
- Not necessarily cumulative: repeatedly adding a very small number to a large number may do nothing.
Example: Non-associative Feature
Find \(a\), \(b\) and \(c\) such that \((a + b) + c \neq a + (b + c)\) under double-precision floating point arithmetic.
Answer
Let \(a = \pi, b = 10^{100}, c = -10^{100}\)Under double-precision floating point arithmetic:
\((a + b) + c = 10^{100} + (-10^{100}) = 0\)
\(a + (b + c) = \pi + 0 = \pi\)
Example: Non-distributive Feature
Find \(a\), \(b\) and \(c\) such that \(c(a + b) \neq ca + cb\) under double-precision floating point arithmetic.
Answer
Let \(a = 0.1, b = 0.2, c = 100\)Under double-precision floating point arithmetic:
\(c(a + b) = 100 \times 0.30000000000000004 = 30.000000000000004\)
\(ca + cb = 10 + 20 = 30\)
Floating Point Arithmetic
The basic idea of floating point arithmetic is to first compute the exact result, and then round the result to make it fit into the desired precision:
\[x + y = fl(x + y)\] \[x \times y = fl(x \times y)\]Floating Point Addition
Adding two floating point numbers is easy. The basic idea is:
- Bring both numbers to a common exponent
- Do grade-school addition from the front, until you run out of digits in your system
- Round the result
Consider a number system such that \(x = \pm 1.b_1 b_2 b_3 \times 2^m\) for \(m \in [-4, 4]\) and \(b_i \in \{0, 1\}\), and we perform addition on two numbers from this system.
Example 1: No Rounding Needed
Let \(a = (1.101)_2 \times 2^1\) and \(b = (1.001)_2 \times 2^1\), find \(c = a + b\).
Answer
\(c = a + b = (10.110)_2 \times 2^1 = (1.011)_2 \times 2^2\)Example 2: No Rounding Needed
Let \(a = (1.100)_2 \times 2^1\) and \(b = (1.100)_2 \times 2^{-1}\), find \(c = a + b\).
Answer
\(c = a + b = (1.100)_2 \times 2^1 + (0.011)_2 \times 2^1 = (1.111)_2 \times 2^1\)Example 3: Requiring Rounding and Precision Lost
Let \(a = (1.a_1a_2a_3a_4a_5a_6...a_n...)_2 \times 2^0\) and \(b = (1.b_1b_2b_3b_4b_5b_6...b_n...)_2 \times 2^{-8}\), find \(c = a + b\). Assume a single-precision system is used, and that \(n \gt 23\).
Answer
In single precision:\(a = (1.a_1a_2a_3a_4a_5a_6...a_{22}a_{23})_2 \times 2^0\)
\(b = (1.b_1b_2b_3b_4b_5b_6...b_{22}b_{23})_2 \times 2^{-8}\)
So \(a + b = (1.a_1a_2a_3a_4a_5a_6...a_{22}a_{23})_2 \times 2^0 + (0.00000001b_1b_2b_3b_4b_5b_6...b_{14}b_{15})_2 \times 2^0\)
In this example, the result \(c = fl(a+b)\) includes only \(15\) bits of precision from \(b\), so a lost of precision happens as well.
Example 4: Require Rounding and Precision Lost
Let \(a = (1.101)_2 \times 2^0\) and \(b = (1.000)_2 \times 2^0\), find \(c = a + b\). Round down if necessary.
Answer
\(c = a + b = (10.101)_2 \times 2^0 \approx (1.010)_2 \times 2^1\)Example 5: Require Rounding and Precision Lost
Let \(a = (1.101)_2 \times 2^1\) and \(b = (1.001)_2 \times 2^{-1}\), find \(c = a + b\). Round down if necessary.
Answer
Example 6: No Rounding Needed but Precision Lost
Let \(a = (1.1011)_2 \times 2^1\) and \(b = (-1.1010)_2 \times 2^1\), find \(c = a + b\).
Answer
\(c = a + b = (0.0001)_2 \times 2^1 = (1.????)_2 \times 2^{-3}\)Unfortunately there is not data to indicate what the missing digits should be. The effect is that the number of significant digits in the result is reduced. Machine fills them with its best guess,which is often not good (usually what is called spurious zeros). This phenomenon is called Catastrophic Cancellation.
Floating Point Subtraction and Catastrophic Cancellation
Floating point subtraction works much the same was that addition does. However, problems occur when you subtract two numbers of similar magnitude.
For example, in order to subtract \(b = (1.1010)_2 \times 2^1\) from \(a = (1.1011)_2 \times 2^1\), this would look like:
When we normalize the result, we get \(1.???? \times 2^{-3}\). There is no data to indicate what the missing digits should be. Although the floating point number will be stored with 4 digits in the fractional, it will only be accurate to a single significant digit. This loss of significant digits is known as catastrophic cancellation.
More rigidly, consider a general case when \(x \approx y\). Without loss of generality, we assume \(x, y \gt 0\) (if \(x\) and \(y\) are negative, then \(y - x = -(x - y) = -x - (-y)\), where \(-x\) and \(-y\) are both positive and similar in magnitude). Suppose we need to calculate \(fl(y - x)\) given:
\[x = 1.a_1 a_2 a_3 ... a_{n-2} a_{n-1}0 a_{n+1} a_{n+2} ... \times 2^m\] \[y = 1.a_1 a_2 a_3 ... a_{n-2} a_{n-1}1 b_{n+1} b_{n+2} ... \times 2^m\]It can be shown that for all \(n \gt 1\), precision lost happens, and it becomes more catastrophic when \(n\) increases (in other words, when \(x\) and \(y\) gets more similar). Then, consider when \(n = 23\) and single-precision floating point system is used, then \(fl(y - x) = 1.????... \times 2^{-23+m}\), where the leading "\(1\)" before the decimal point becomes the only significant digit. Notice that the floating point system may produce \(fl(y - x) = 1.000... \times 2^{-n+m}\), but all digits after the decimal point are "guessed" and are not significant digits. In fact, the precision lost is not due to \(fl(y-x)\) but due to rounding of \(x, y\) from the beginning in order to get numbers representable by the floating point system.
Example: Using Mathematically-Equivalent Formulae to Prevent Cancellation
Consider the function \(f(x) = \sqrt{x^{2} + 1} - 1\). When we evaluate \(f(x)\) for values of \(x\) near zero, we may encounter loss of significance due to floating point subtraction. If \(x = 10^{-3}\), using five-decimal-digit arithmetic, \(f(10^{-3}) = \sqrt{10^{-6} + 1} - 1 = 0\). How can we find an alternative formula to perform mathematically-equivalent computation without catastrophic cancellation?
Answer
A method of avoiding loss of significant digits is to eliminate subtraction:\( f(x) = \sqrt{x^{2} + 1} - 1 = \frac{ (\sqrt{x^{2} + 1} - 1) \cdot (\sqrt{x^{2} + 1} + 1) } { \sqrt{x^{2} + 1} + 1 } = \frac{ x^{2} } { (\sqrt{x^{2} + 1} + 1) } \)
Thus for \( x = 10^{-3} \), using five-decimal-digit arithmetic, \( f(10^{-3}) = \frac{ 10^{-6} } { 2 } \).
Example: Calculating Relative Error when Cancellation Occurs
If \(x = 0.3721448693\) and \(y = 0.3720214371\), what is the relative error in the computation of \((x − y)\) in a computer with five decimal digits of accuracy?
Answer
Using five decimal digits of accuracy, the numbers are rounded as:\(fl(x) = 0.37214\) and \(fl(y) = 0.37202\)
Then the subtraction is computed:
\(fl(x) − fl(y) = 0.37214 − 0.37202 = 0.00012 \)
The result of the operation is:
\(fl(x − y) = 1.20000 × 10^{−2}\)
Notice that the last four digits are filled with spurious zeros.
The relative error between the exact and computer solutions is given by:
\( \frac{\vert (x - y) - fl(x - y) \vert}{\vert (x - y) \vert} = \frac{0.0001234322 − 0.00012}{0.000123432} = \frac{0.0000034322}{0.000123432} \approx \bf{3 \times 10^{-2}} \)
Note that the magnitude of the error due to the subtraction is large when compared with the relative error due to the rounding, which is:
\( \frac{\vert x - fl(x) \vert}{\vert x \vert} \approx 1.3 \times 10^{-5} \)
Review Questions
- Given a real number, what is the rounding error involved in storing it as a machine number? What is the relative error?
- How can we bound the relative error of representing a real number as a normalized machine number?
- What is cancellation? Why is it a problem?
- What types of operations lead to catastrophic cancellation?
- Given two different equations for evaluating the same value, can you identify which is more accurate for certain x and why?